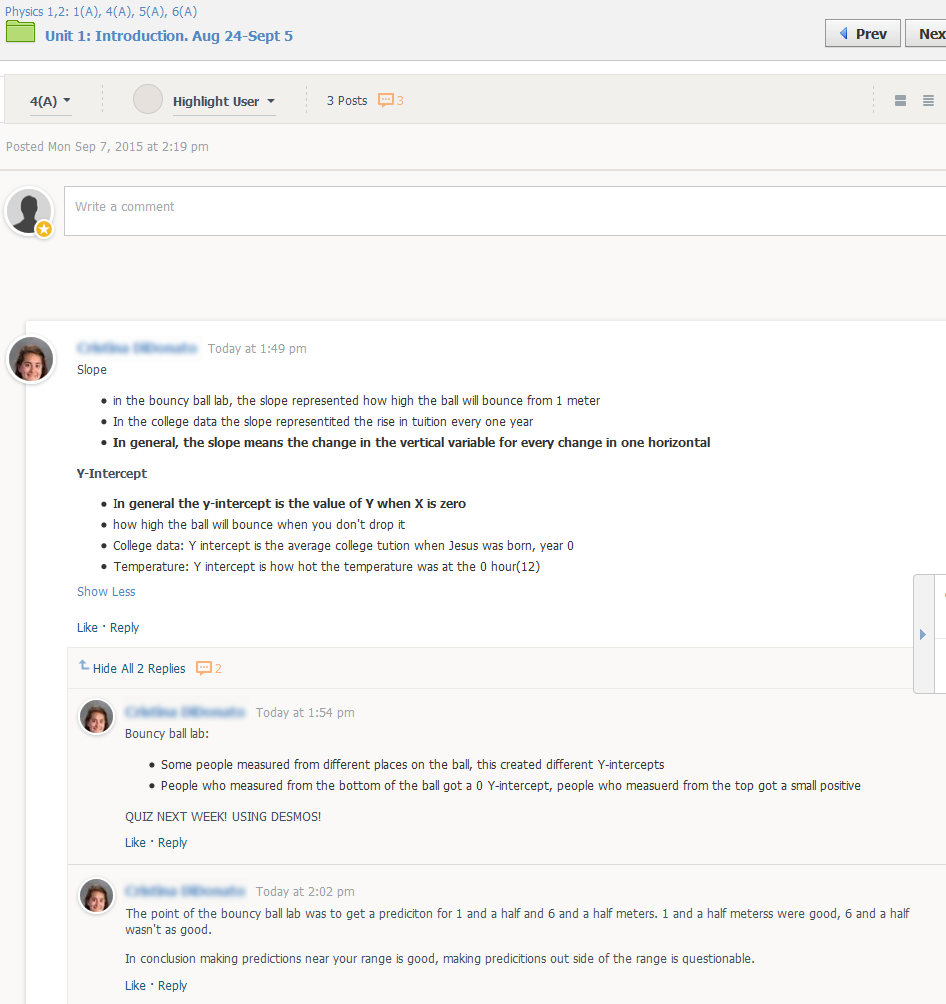
180: Day 11: Unit summaries online
There has been debate in the Modeling Instruction community over how to handle “summaries” at the end of labs/units. We like summaries because they provide our students a place to go to see conclusions that are agreed to as a class–but we worry about them because students may not be as engaged in the labs/discussions if they know the “answers”...