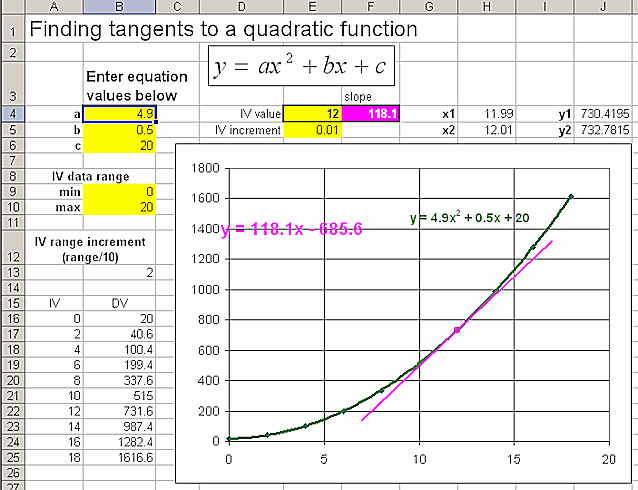
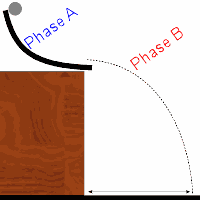
Modeling Instruction: Review of acceleration lab
I’ve been using Modeling Instruction in my physics class for the past five years, and keep wondering how to handle the problem of students who miss the whiteboard sessions (where students share their results and we reach class conclusions). These sessions are critical for student growth, as this is where they are challenged to look for patterns in their data,...