How close are you? The “Why” behind Percent Error
There’s an old saying, “Close only counts in horseshoes and hand grenades.” People would say this in response to someone saying “Well, I was close.” So, why does close count in horseshoes and hand grenades, and why is this the introduction to a science paper?
Horseshoes: If you’ve never played before (I bet most of you haven’t), the goal is to throw a horseshoe towards a pipe in the ground and have the shoe end up around the pipe. You score if the shoe is around the pipe, but you also score if your horseshoe is closer than one horseshoe away. Thus, close counts in the game of horseshoes.
I think we can all understand how close could count with a hand grenade.
“Close” in science
In science, you may run an experiment in which you make measurements and are able to compare that to some “true” value. This tends to be one of two types:
- You make a prediction and then test that prediction (e.g. at what position will these two toy cars collide)
- You calculate a value and compare it to a known value (e.g. you calculate the molarity of a salt solution and compare that to the value your teacher knows).
Let’s examine an example of the second option. Say you calculate the molarity (concentration) of a solution that your teacher knows the molarity of. You carefully measure and calculate, and get a result of 0.75 moles/liter (M). Your teacher says the actual answer is 0.80 M, so you are 0.05 M off. Another group, looking at another solution, gets a result of 0.20 M, and the teacher says the actual answer is 0.15 M, also 0.05 M off. So are you both the same “accuracy?” You may already be saying
"Hmm, 0.05 out of 0.80 seems much closer than 0.05 out of 0.15."
A sidetrack to grades, before we go on…
You may also experience this with tests. If you scored 93 out of 100 points on a test, you know quickly that you earned a 93% on that test. But if you score 67 out of 75 points, it’s not so quick. You can probably quickly calculate your percent, using the formula:
$latex \frac{67}{75}=\frac{?}{100}&s=3&bg=35302E&fg=ffffff$
The grade on this test is 89.3%
Let’s take a look at that word “percent.” It means just what it looks like “per hundred.” What you do when you calculate a percentage is you say “if this test were out of 100, my score would be…” If this test had been worth 100 points, the score would be 89.3.
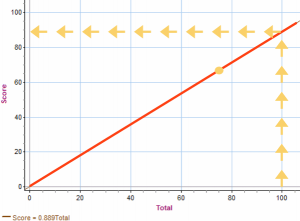
You could solve this using a graph:
The graph shows the score (67 out of 75), then a red line from (0,0) going through that point. This red line shows the scores that anyone who gets the same ratio (score out of total) will land on. We can then start at 100 points Total, draw a line up to the red line, then left to find the score for 100: About 90%–very close to our mathematically calculated 89.3%
Back to percent error and our salt solution
If both salt solutions had the same molarity, we could just compare results (e.g. the solution is 1.2, and I got 1.1 and you got 1.0, clearly I am closer). But, we want a way to compare different molarities–just like converting tests with different total points to percentages helps us compare our results on all tests. Calculating percent error is how scientists do this. But, instead of saying “I did well, I got a 98%,” scientists say “I did well, I was only 2% off.” So the calculation, instead of using the experimental value, uses the difference between the experimental value and the known value.
Let’s look at our first concentration result:
$latex \frac{\lvert0.75-0.80\rvert}{0.80}=\frac{?}{100}&s=3&bg=35302E&fg=ffffff$
Notice the absolute value bars? When reporting your percent error, it generally doesn’t matter if we are above or below the known/standard number, so we drop the sign and report it all as positive.
Note: Using the absolute value is the traditional way of reporting percent error. However, it may be valuable to keep and report the sign, especially when comparing different lab groups’ results in a class. If everyone’s error has the same sign, this can lead to a discussion evaluating the experimental design to hypothesize factors that may cause the experimental results to be consistently greater or less than the predicted/known results.
So, the percent error for the first result is 6.25%. Let’s look at our second result:
$latex \frac{\lvert0.20-.15\rvert}{0.15}=\frac{?}{100}&s=3&bg=35302E&fg=ffffff$
The percent error for this result is 33.3%.
In conclusion
Back to our example, both groups’ results were “only 0.05 M” off. But the percent errors are not the same. It is by calculating the percent error that we can recognize how different these two results are.
One last example that may help clarify the importance of thinking about differences as a percent: Let’s say I’m going to pay you for some work you do, but I tell you I may be $20-30 off of what I actually owe you. If I owe you $50, you would likely be really bothered if I short-changed you $20, and you only get $30. But if I owe you $5,000, you probably won’t as bothered if I only give you $4,980 (also $20 short). The “experimental error” in the first payment is 40%, but for the second payment it’s only 0.04%.
Small differences in small numbers are important, but small differences in large numbers are not so important. Percent error helps us to see this quickly.
