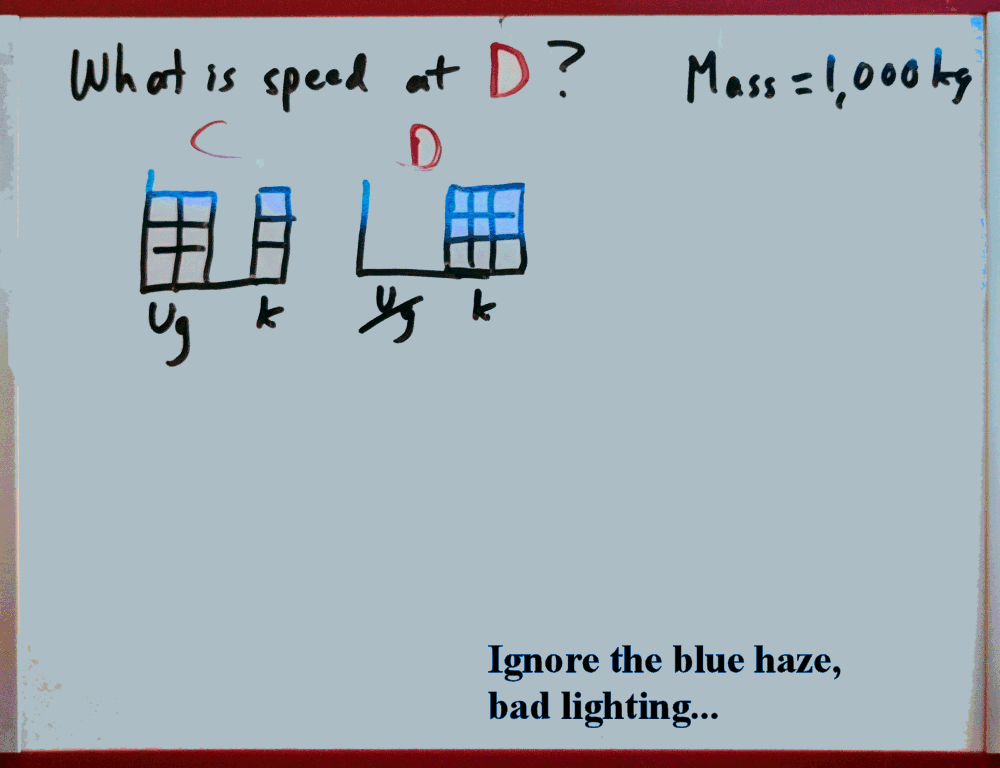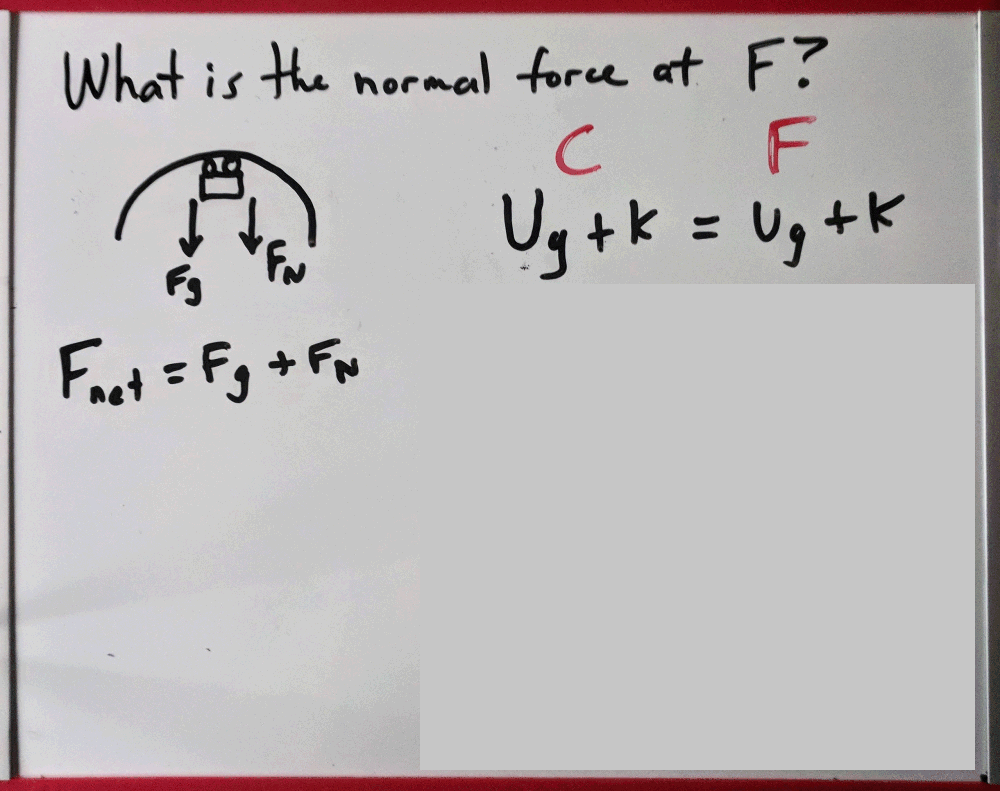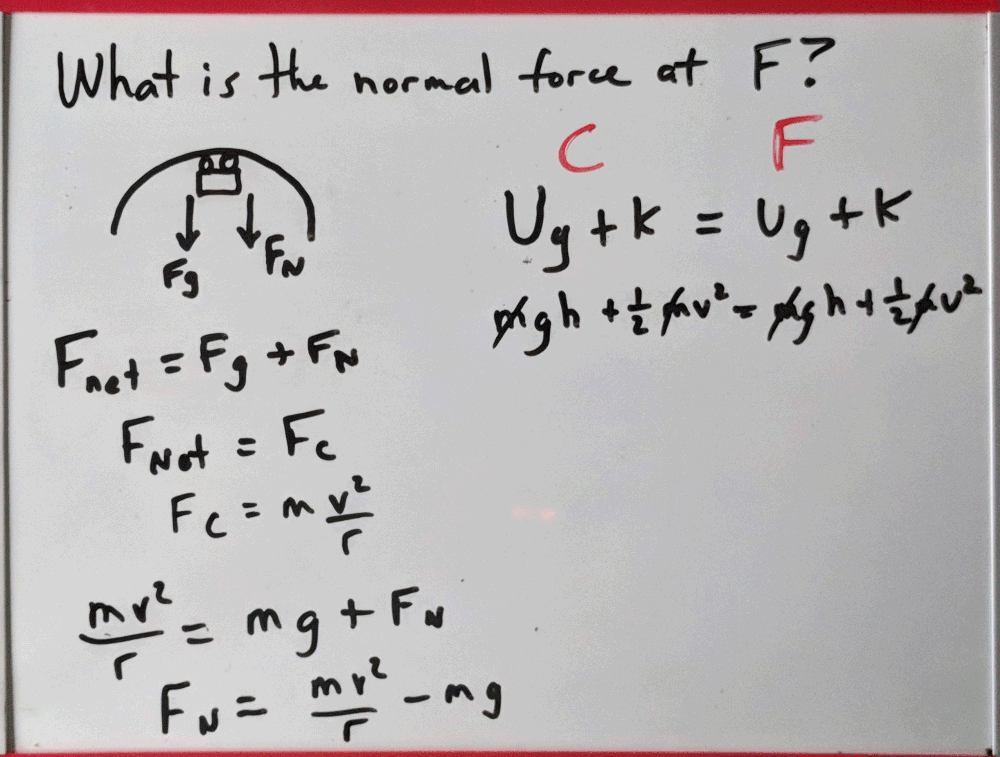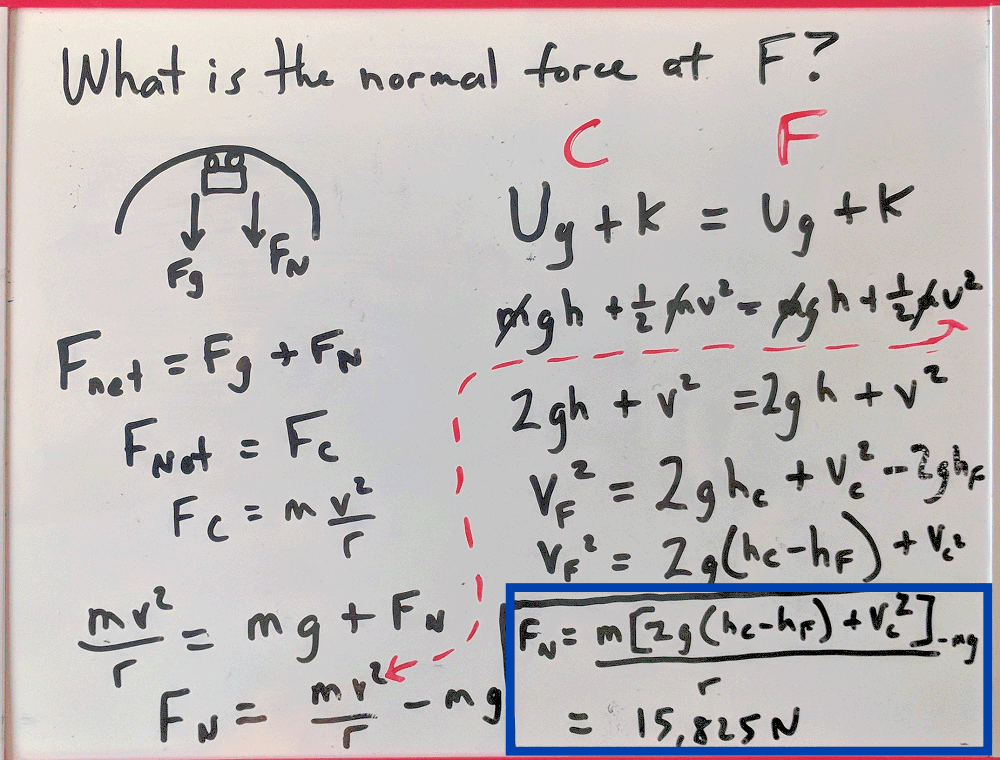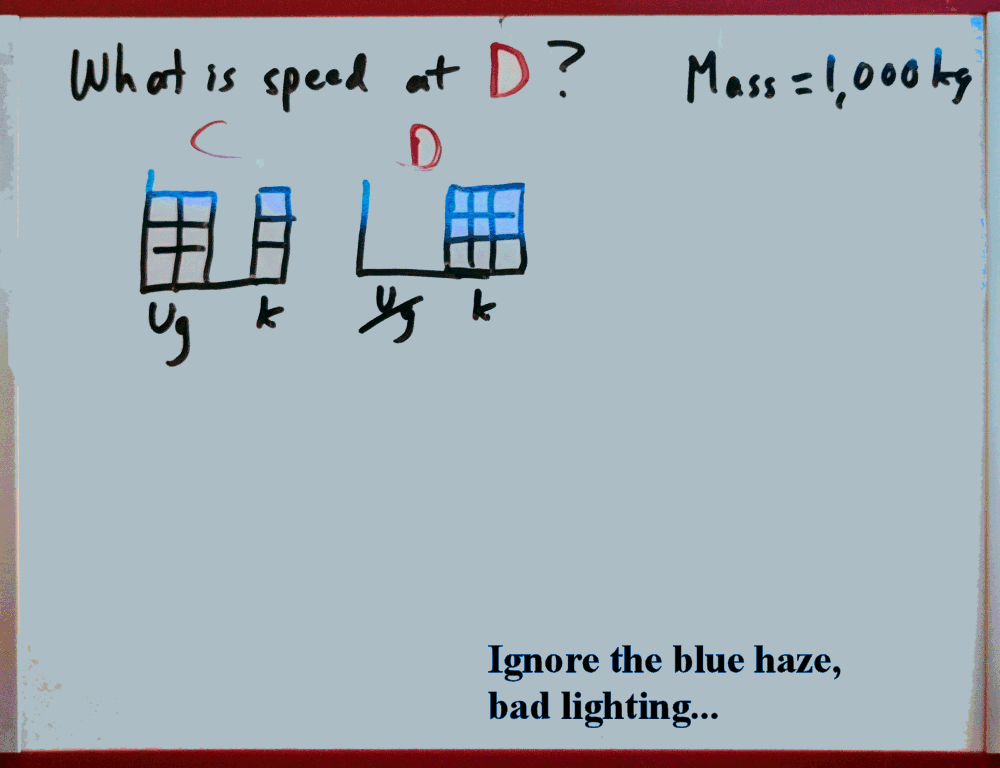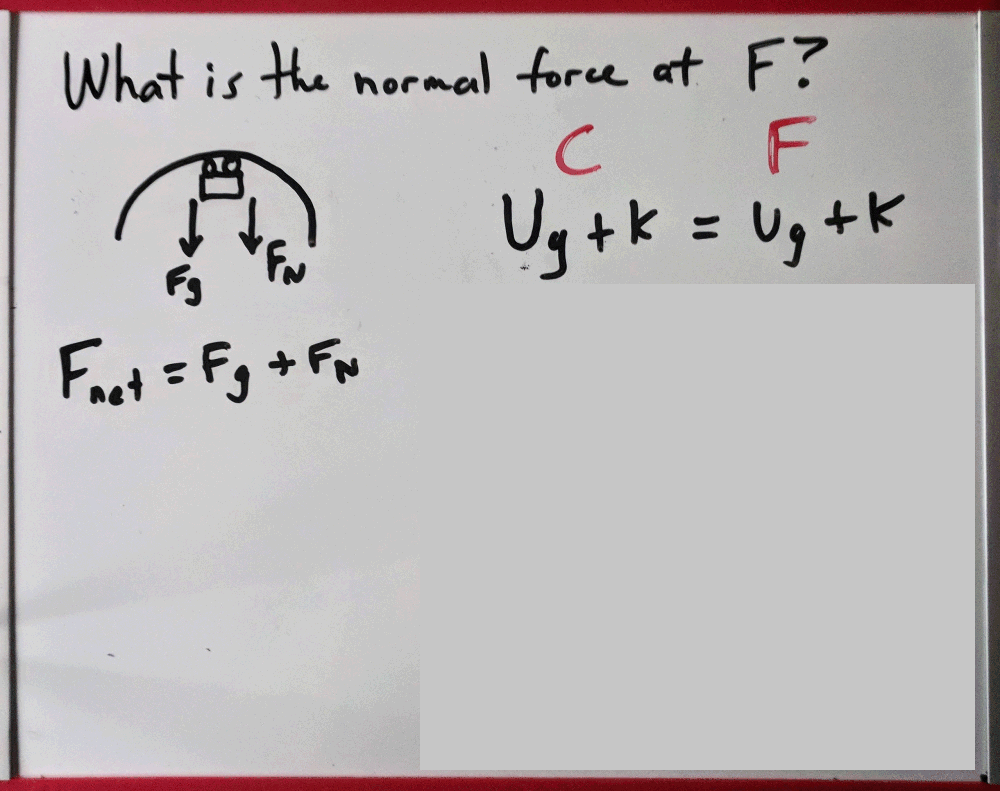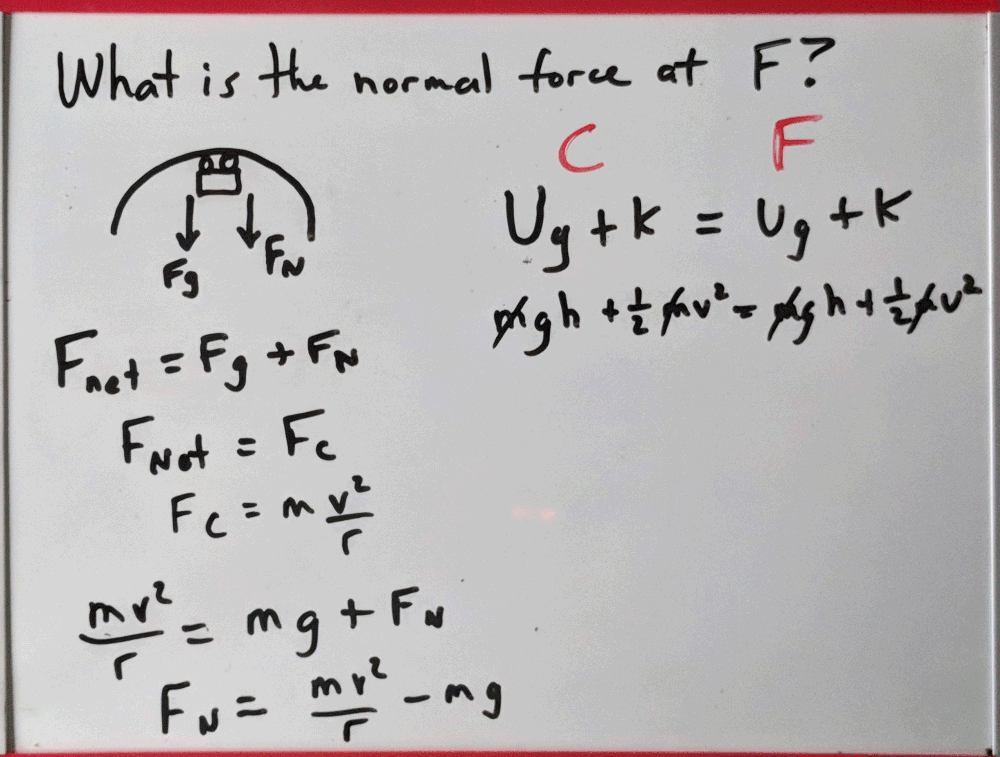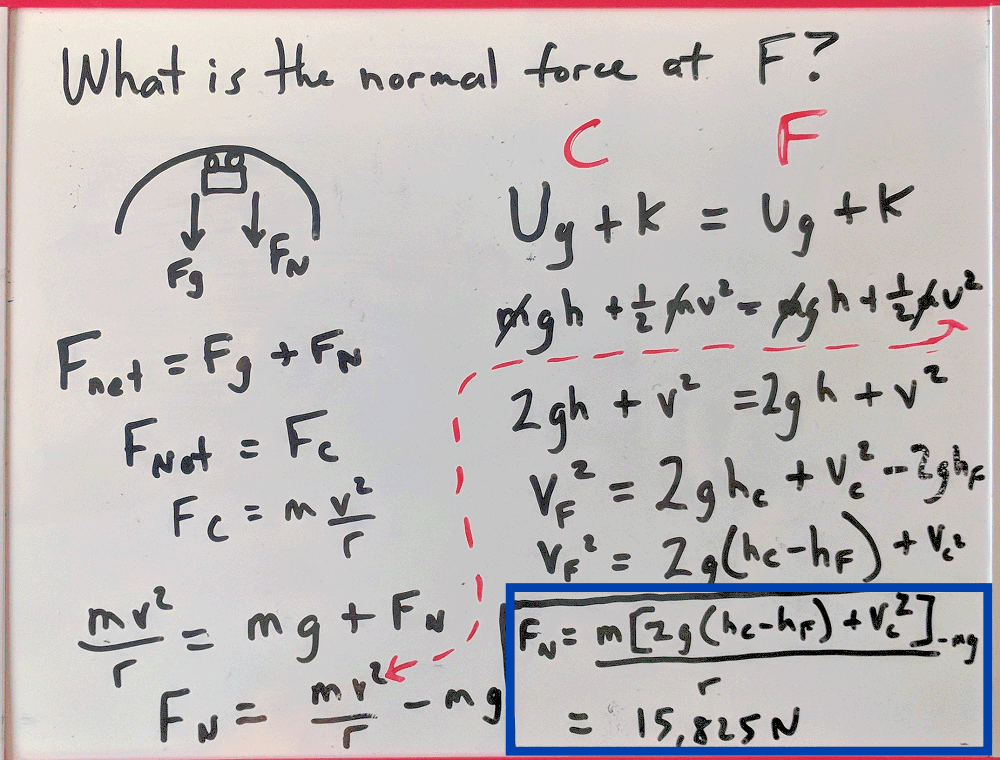Solving ‘roller coaster’ energy problems
Step-by-step instructions.
Try to complete each section on your own before you move to the next image. Each slide shows the answer to the preceding question.
1. First, examine the problem and determine the energy storage types involved.
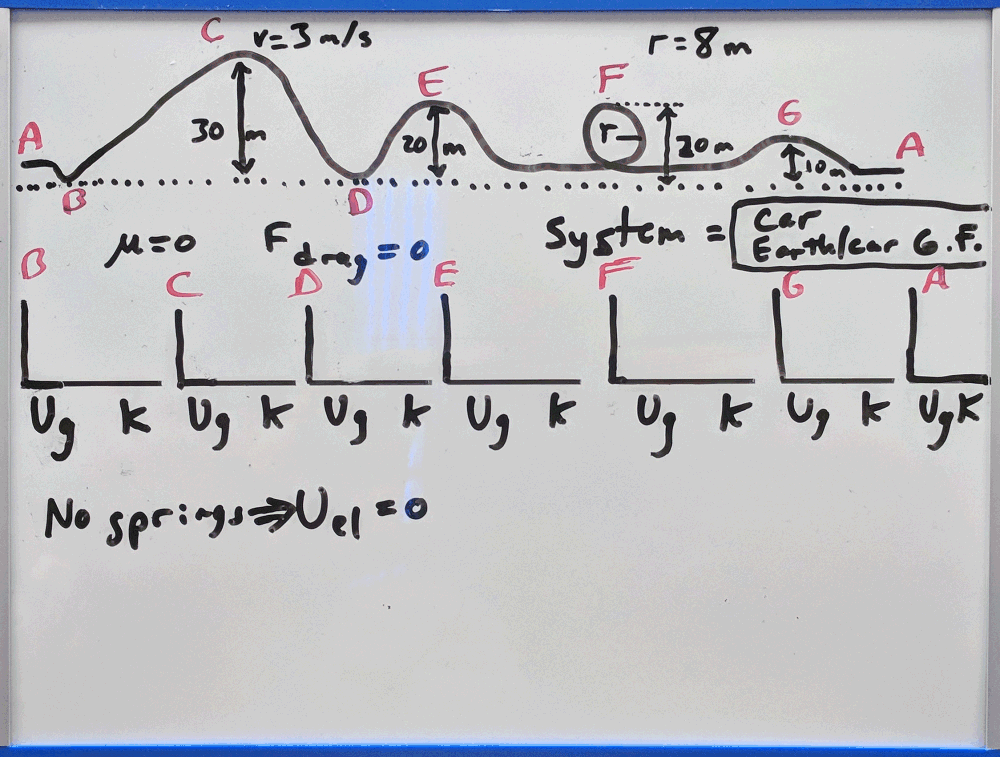
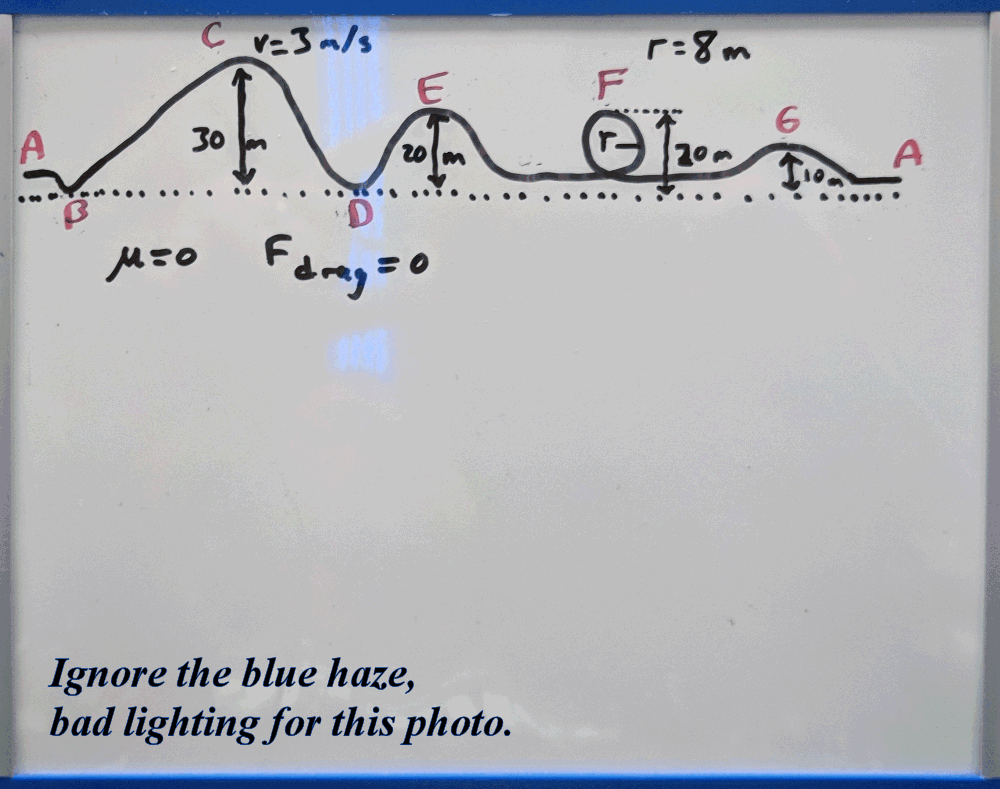 This problem consists of a roller coaster which has a chain that pulls the car to the top of the first hill. The problem defines the system as frictionless (μ = 0), and insignificant air resistance.
This problem consists of a roller coaster which has a chain that pulls the car to the top of the first hill. The problem defines the system as frictionless (μ = 0), and insignificant air resistance.
Before you go on, define the system, then draw axes for your energy diagrams at each point with a letter (don’t worry about the number of blocks of each energy storage yet).
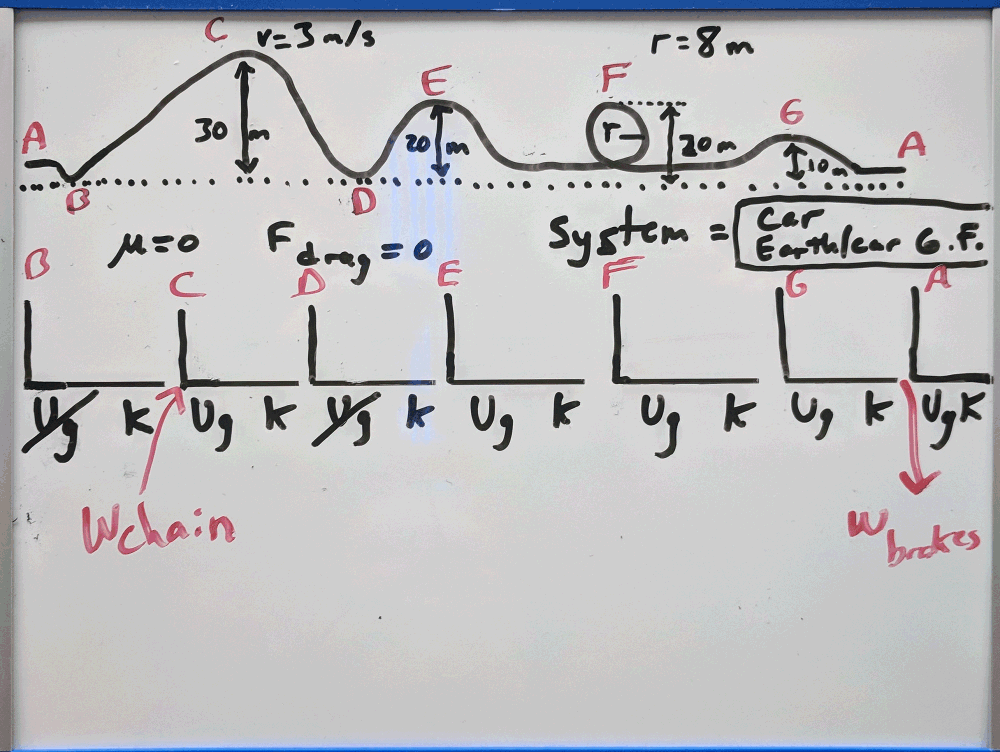
2. Determine where energy must be added or removed from the system.
How did the car get up the first hill? How does the car come to a stop at the end?
Before you go on, add working arrows pointing into or out of the system.
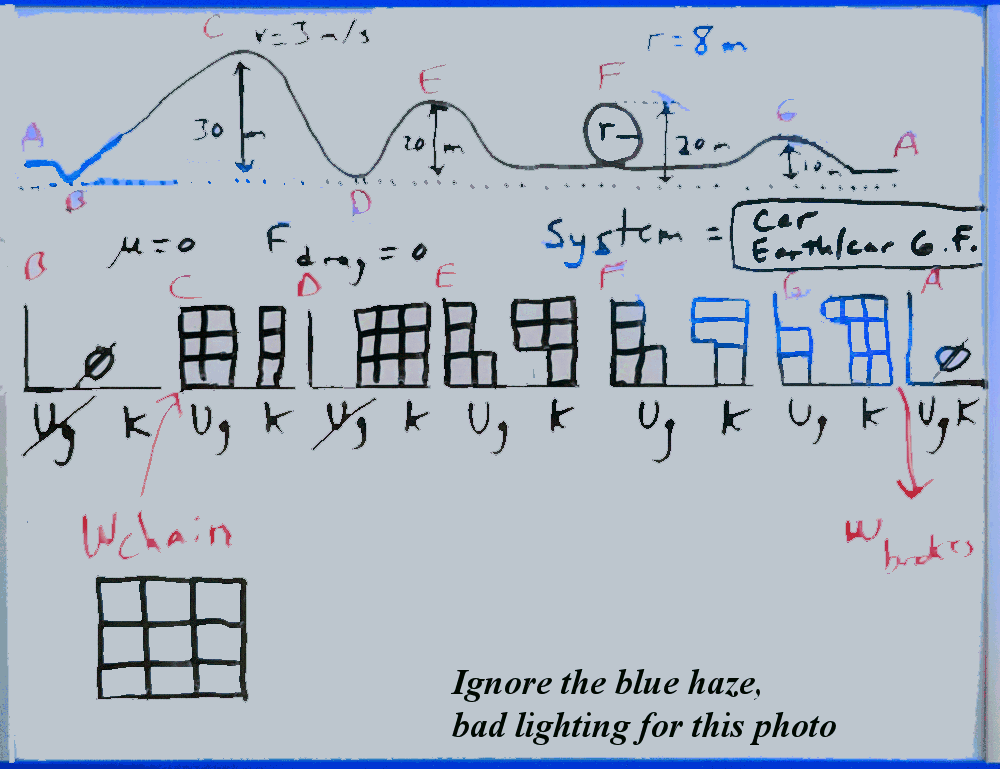
3.  Add blocks to represent units of energy on each graph.
Add blocks to represent units of energy on each graph.
Remember that at this point, we are not worried about the exact amount of energy stored in each type; we just need to make sure that Ei + W − Ediss = Ef for each transaction.
Before you go on, add your energy blocks to each graph.
4. Look at the problem and determine which points in time can be used to answer the question.
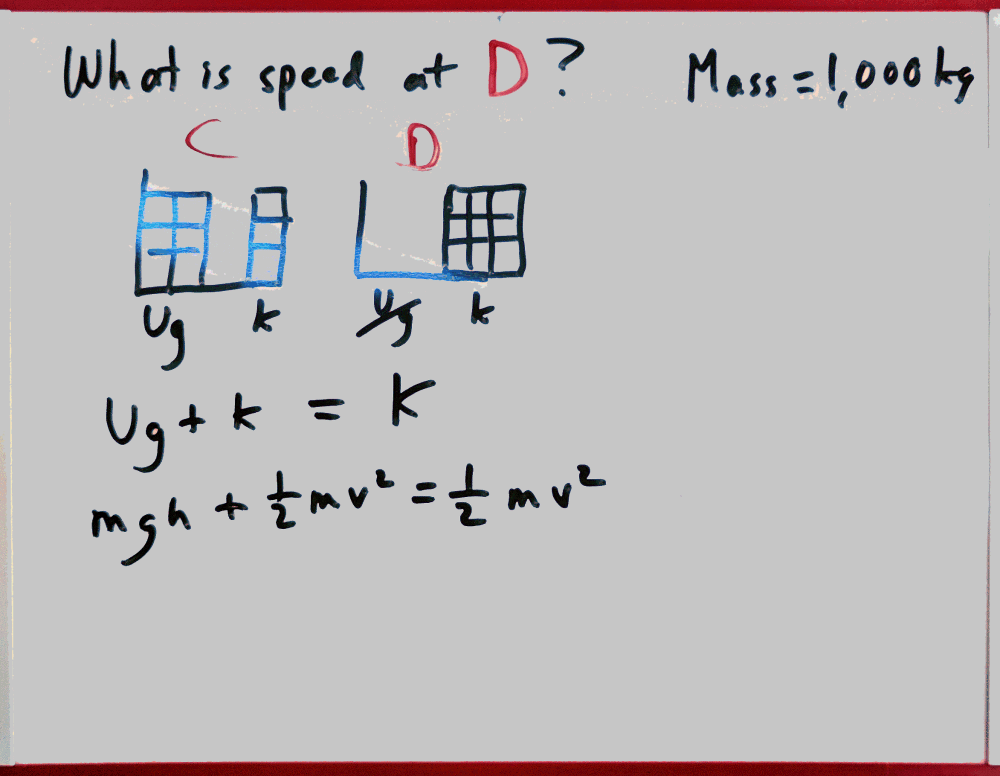
Here is the next question, and the energy storage diagrams from the two points of concern.
Since this question asks about the speed at Point D, we can select that point and C, since we know both the speed and height at C.
Before you go on, write out the balanced energy equation for Points C and D.
5. Rearrange your equations to solve for unknown, then enter your values and solve.
Before you go on, rearrange the equation to solve for vD, then plug in your numbers and solve.
6. Your done!
Before you go on, check to make sure your answer is reasonable.
Since the car started at 3 m/s at the top of the hill, 24.4 m/s seems ‘reasonable’ for the bottom of the hill. (Remember the shortcut that m/s*2≈MPH, so 24.4*2 ≈48.8 MPH, a nice, fast roller coaster.)
7. Here’s another problem involving the loop.
Try it out using the above steps (but remember, since it involves centripetal forces, you will need to use Fc = (mv2)/r = Fnet.
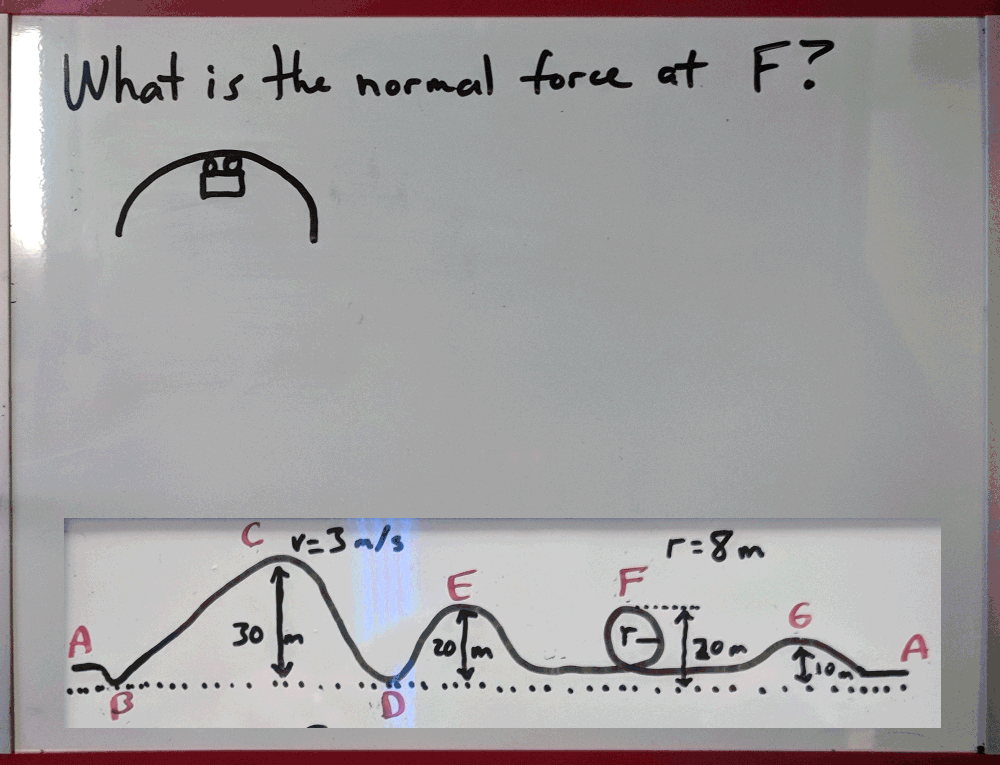
Before you scroll down,draw a force diagram for the car and an energy equation for two locations.
8. Expand all your equations and rearrange them to solve for the unknown.
9. Combine your energy and force equations
10. Solve!
11. You are done.
Once again, does this answer seem correct? Compare it to the normal force of the cart just resting on the ground.